Question

A certain model of a passenger car has two types: four-door and two-door cars. Suppose 60% of the cars in this model are four-door cars. The two types of cars in this model will be randomly delivered to a certain dealer one by one in a particular week. Zachary wants to buy a two-door car in the model from this dealer, so he asked the dealer to notify him when the first two-door car is delivered. a. Find the probability that the first two-door car is the third one in this model delivered to this dealer this week. b. Find the expected number of cars in this model until the first two-door car is delivered in this week.

Answer 1

a) There is a 14.4% probability that the first two-door car is the third one in this model delivered to this dealer this week.

b) The expected number of cars in this model until the first two-door car is delivered in this week is 2.5.

Explanation:

The negative binomial distribution allows us to find the number of failures before a success.

It has parameters n and p, in which n is the number of trials and p is the probability of a success.

The probability that it takes n trials for x sucesses is given by the following formula:

`P = C_(n-1, x-1)*(p)^x*(1-p)^(n-x)`

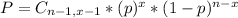
In which C_{(n-1),(x-1)} is the number of different combinatios of x-1 objects from a set of n-1 elements, given by the following formula.

`C_(n,x) = ((n-1)!)/((x-1)!(n-x)!)`

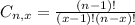
a. Find the probability that the first two-door car is the third one in this model delivered to this dealer this week.

There is a 40% that a car is a two-door car, so
`p = 0.4`

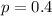
We want it to take 3 trials for a sucess, so
`n = 3, x = 1`.

`P = C_(n-1, x-1)*(p)^x*(1-p)^(n-x)`

`P = C_(2, 0)*(0.4)^1*(0.6)^(2) = 0.144`

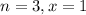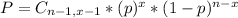
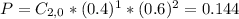
There is a 14.4% probability that the first two-door car is the third one in this model delivered to this dealer this week.

b. Find the expected number of cars in this model until the first two-door car is delivered in this week.

The expected number of trials for r sucesses with p probability is given by the following formula.

`\mu = (r)/(p)`.

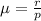Here, we want the expected number of trials for 1 sucess, with 0.40 probability.

S

`\mu = (1)/(0.4) = 2.5`

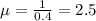
The expected number of cars in this model until the first two-door car is delivered in this week is 2.5.