Question

A factory employs several thousand workers, of whom 35% are Hispanic. If the 17 members of the union executive committee were chosen from the workers at random, the number of Hispanics on the committee would have the binomial distribution with n = 17 and p = 0.35. (a) What is the mean number of Hispanics on randomly chosen committees of 17 workers? (b) What is the standard deviation σ of the count X of Hispanic members? (c) Suppose that 10% of the factory workers were Hispanic. Then p = 0.1. What is σ in this case? What is σ if p = 0.01? What does your work show about the behavior of the standard deviation of a binomial distribution as the probability of a success gets closer to 0? As p decreases, σ decreases. As p increases, σ increases. As p increases, σ decreases. As p decreases, σ increases.

Answer 1

as p decreases, sigma decreases.

Explanation:

Given that 35%are hispanic. For a sample of 17 members

n = 17

p = 0.35

and the number of Hispanics on the committee would have the binomial distribution

a) Mean of X = E(x) =
`np = 17(0.35)\\= 5.95`

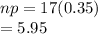
b) Std dev X =
`√(npq) =√(5.95(0.65)) \\=1.9665`

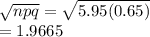
c) Here n =17 and p =0.1

`Mean = 1.7\\\sigma = √(17(0.1)(0.9)) =1.234`

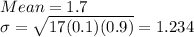
d) When p = 0.01

`Mean = 0.17\\\sigma = 0.410`

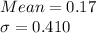
Thus we find that as p decreases, sigma decreases.