Question

Joy kayaked up the river and then back in a total time of 6 hours. The trip was 4 miles each way. The current was difficult. If joy kayaked at a speed of 5 mph in still water, what is the speed of the current?

Answer 1

The speed of the current is 5 miles per hour.

Explanation:

Given, Joy kayaked up the river and then back in a total time of 6 hours.

The trip was 4 miles each way.

The current was difficult.

Let the speed of current be 'a' miles per hour

If joy kayaked at a speed of 5 mph in still water, we have to find what is the speed of the current?

Now, we know that,

distance = speed x time

So,

`time =( Distance)/(speed)`

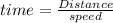
Then, total time = time for up stream + time for down stream

`6 hours = \frac{(4 miles)}{(a-\text{5 miles per hours})} +\frac{ (4 miles)}{(a+\text{5 miles per hour})}`

`6 = (4)/((a-5))+  (4)/((a+5))`

`( 6)/(4)= ( 1)/((a-5))+ ( 1)/((a+5))`

`(3)/(2)= ( (a+5+a-5))/(((a-5)(a+5)))`

`( 3)/(2)= ( 2a)/((a^2- 5^2 ))`

`3(a^2- 25) = 4a`

`3a^2 -4a -75 = 0`

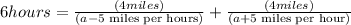
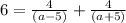
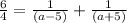
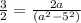
Now, let us use quadratic formula,
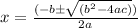`x =( (-b\pm√((b^2-4ac))))/(2a)` to find a value.

Then,
`a = ((-(-4)\pm√((-4)^2-(4 * 3 *(-75))))/((2 * 3))`

`A = ((4\pm√((16+ 12 x 75))))/(6)`

`A =( (4\pm√(916))/(6)`

`A =( (4 \pm 30.265))/(6)`

`A =( 34.2656)/(6)`

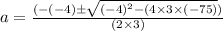
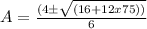
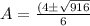
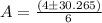
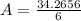
we can neglect – ve values of speed.

A = 5.71