Answer: N(20, 4) distribution.
Explanation:
Normal approximation to Binomial :
The normal approximation is used for binomial distribution having parameters n and p as
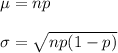
if x is the random variable then x has
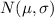 .
.
Given : As part of a promotion for a new type of cracker, free trial samples are offered to shoppers in a local supermarket.
The probability that a shopper will buy a packet of crackers after tasting the free sample : p=0.20.
Different shoppers can be regarded as independent trials.
if X is the number among the next 100 shoppers who buy a packet of crackers after tasting a free sample.
Then, Mean and standard deviation for x will be :
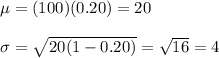
i.e. X has approximately an N(20, 4) distribution.