Answer:
The speed of the combined honey drop after the collision is 9.05 m/s.
Step-by-step explanation:
Given that,
The masses and velocities of the drops are
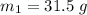
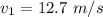
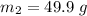
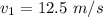

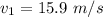
We need to calculate the total mass
Using formula of masses
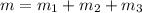
Put the value into the formula
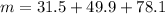
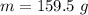
We need to calculate the velocity in x- direction
Using conservation of momentum
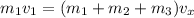

Put the value into the formula
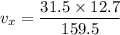

We need to calculate the velocity in y- direction
Using conservation of momentum
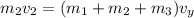
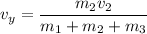
Put the value into the formula
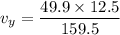
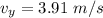
We need to calculate the velocity in z- direction
Using conservation of momentum
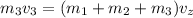
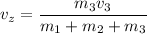
Put the value into the formula

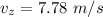
We need to calculate the combined honey drop after the collision
Using formula of velocity
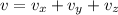
Put the value into the formula
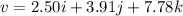
The magnitude of velocity
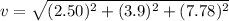
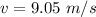
Hence, The speed of the combined honey drop after the collision is 9.05 m/s.