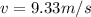Answer:
1.
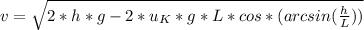
2.
Step-by-step explanation:
1.
Kinetic energy and potential energy describe the motion also the small push means that initial kinetic energy is considered zero so:
Work done=Potential energy-Kinetic energy

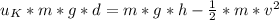
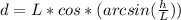
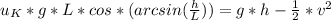
Solve to v
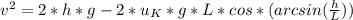
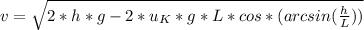
2.
Replacing the given: to find speed at the bottom