Answer: 2051.64 kilowatt hours.
Explanation:
Given : Sample size : 44
The sample mean :
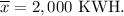
Population standard deviation:
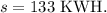
z-value for 99% confidence interval :
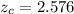
The upper bound of the 99% confidence interval estimate for the population mean :-
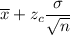

Hence, the upper bound of the 99% confidence interval estimate for the population mean = 2051.64 kilowatt hours.