Question

QUESTION 3 Graph of a line containing the following points: (–3, –4) and (1, –4). Which is the equation of the given line? x = –4 y = –4 y = –4x x = 4

Answer 1

y = -4

Explanation:

We can find the equation of a line that goes through two given points on the plane by finding 1) the slope of the segment that joints the two points, and using the coordinates of one of the given points, and use this information in the "point-slope" form of the line.

To find the slope of the segment that joins the two points, we use the general equation for the slope given two coordinate pair points
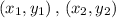`(x_1,y_1)\,,\,(x_2,y_2)` as:
`slope=(y_2-y_1)/(x_2-x_1)`

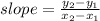
In our case, using the given (-3,-4) as
`(x_1,y_1)`, and (1,-4) as
`(x_2,y_2)`, we get the following slope:

`slope=(y_2-y_1)/(x_2-x_1)\\slope=(-4-(-4))/(1-(-3))\\\\slope=(-4+4)/(1+3)\\slope=(0)/(4)=0`

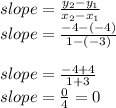
Therefore, the slope is zero (this means we are dealing with a horizontal line.

Now we complete the work by using the point-slope form of a line which is:

`y-y_0=m(x-x_0)`

Using one of the given points (let's say (1,-4) as
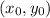`(x_0,y_0)`, and the slope (0) that we just obtained, we get the following equation for the line in question:

`y-y_0=m(x-x_0)\\y-(-4)=0(x-1)\\y+4=0\\y=-4`

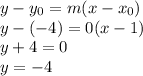
So y = -4 is the expression for the line