Question

How high can a roller coaster be? A roller coaster car is to roll down a frictionless ramp into a loop of a radius r. If the riders can withstand an acceleration of 9g's and not black out - i.e. their apparent weight at the bottom of the loop is nine times their actual weight; what is the maximum height of the incline if the cars starts from the rest?

Answer 1

h=4r

Step-by-step explanation:

To solve the problem it is necessary to apply the energy conservation equations for the roller coaster.

The energy conservation equations warn that:

`\Delta KE = \Delta PE`

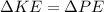
Where,

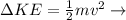`\Delta KE = (1)/(2) mv^2 \rightarrow` Kinetic Energy

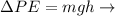`\Delta PE = mgh \rightarrow` Potential Energy

Equating,

`(1)/(2)mv^2 = mgh`

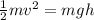
Re-arrange for V,

`V^2 = 2gh`

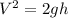
For balance of forces, according to the announcement, those who are on a roller coaster can withstand up to a maximum of 9g.

Therefore, considering the centripede speed and the speed of the fall, we obtain that,

`F_w+F_a = F_t`

`mg+ma = 9mg`

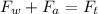
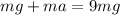
The centripetal acceleration is given by the equation

`a = (V^2)/(r)`

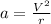
Where

V = Tangencial velocity

r = Radius

Then replacing in the equation of Force,

`mg + m(V^2)/(r) = 9mg`

`mg + m ((2gh))/(r) = 9mg`

`1+(2h)/(r) = 9`

`h= (8r)/(2)`

`h= 4r`

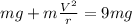
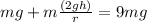
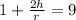
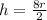
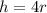
Therefore the maximum height of the incline if the cars starts from the rest is 4 times the raidus of the inclination