Question

Joe's starting salary is $80,000 per year. He plans to put 10% of his salary each year into a mutual fund. He expects his salary to increase by 5% per year for the next 30 years, and then retire. If the mutual fund will average 7% annually over the course of his career, how much money will he have to retire on?

Answer 1

Joe will have approximately $78,122.37 to retire on.

Step-by-step explanation:

To calculate how much money Joe will have to retire on, we can use the formula for compound interest: A = P
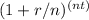`(1 + r/n)^((nt))`, where A is the future amount, P is the principal (initial amount), r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years. In this case, Joe's principal is 10% of his salary, which is $80,000 x 0.10 = $8,000. The annual interest rate is 7%, and the number of times interest is compounded per year is 1. Joe plans to save for 30 years, so t = 30. Plugging these values into the formula, we get A = $8,000
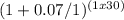`(1 + 0.07/1)^((1 x 30))`. Using a calculator, we find that Joe will have approximately $78,122.37 to retire on.

Answer 2

FV= $1,930,661.48

Step-by-step explanation:

Giving the following information:

Joe's starting salary is $80,000 per year. He plans to put 10% of his salary each year into a mutual fund. He expects his salary to increase by 5% per year for the next 30 years, and then retire. If the mutual fund will average 7% annually

We need to use the following formula:

FV= {A*[(1+i)^n-1]}/i

A= annual deposit

FV= {8000*[(1.12^30)-1]}/0.12= $1,930,661.48