Question

One of the most important properties of materials in many applications is strength. Two of the qualitative measures of the strength of a material are tensile strength and shear strength. The tensile strength of a material is the amount of force needed to pull the material apart perpendicular to a cross section, such as pulling on a rope. The shear strength is the amount of force needed to rupture the material when a force is applied parallel to the cross section, such as breaking a pencil overhanging a table edge. Both tensile strength and shear strength have units of pressure, because they represent the force that must be applied per unit area in order to break the material. The importance of knowing the tensile strength and shear strength of a material is evidenced by the number of machines and companies specializing in determining these properties. Many types of materials and objects are tested, from fabric and metal to nuts and bolts. It is always comforting to know that the tensile strength of the rope holding you above the ground can support your weight. Shear strength needs to be found for bridges, the floors of multilevel buildings, and the joints where the wings join the body of an airplane. Without the experimental determination of these properties, trial and error would be the only other method of determining these values, a process that would be dangerous to life and limb.

QUESTION A) Given that the tensile strength of aluminum foil is 311 megapascals, its thickness is approximately 15.0 micrometers, and a roll of household aluminum foil is 30.0 centimeters wide, how much force F is needed to pull off a sheet to use?

Assume that the force is applied equally along the whole width of the foil, and that you are trying to pull perpendicular to the cross section.

QUESTION B)

As stated in the introduction, shear strength is another measure of the strength of a material. A shear force is a force that acts parallel to the plane in the material that breaks. A good example of a shear is that of a martial arts expert breaking boards or bricks with her hands. Other applications in which shear forces and shear strength need to be known are geology, for studying earthquakes and landslides; fluid dynamics; and structural engineering.

Aluminum has a shear strength of 210 megapascals. When you bend aluminum foil around an edge (i.e., the edge of the box) and pull, you are effectively applying a shear force along the bent edge of the foil. If a roll of household aluminum foil is 30.0 centimeters wide and its thickness is approximately 15.0 micrometers, how much shear force is needed to pull off a sheet?

Assume that the force is applied equally along the whole width of the foil.

Answer 1

To solve this exercise it is necessary to take into account the concepts related to Tensile Strength and Shear Strenght.

In Materials Mechanics, generally the bodies under certain loads are subject to both Tensile and shear strenghts.

By definition we know that the tensile strength is defined as

`\sigma = (F)/(A)`

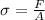
Where,

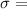`\sigma =`Tensile strength

F = Tensile Force

A = Cross-sectional Area

In the other hand we have that the shear strength is defined as

`\sigma_y = (F_y)/(A)`

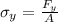
where,

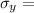`\sigma_y =`Shear strength

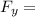`F_y =` Shear Force

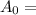`A_0 =`Parallel Area

PART A) Replacing with our values in the equation of tensile strenght, then

`311*10^6 = (F)/((15*10^(-6))(30*10^(-2)))`

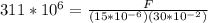
Resolving for F,

`F= 1399.5N`

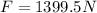
PART B) We need here to apply the shear strength equation, then

`\sigma_y = (F_y)/(A)`

`210*10^6 = (F_y)/(15*10^(-6)30*10^(-2))`

`F_y = 945N`

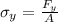
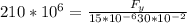
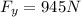
In such a way that the material is more resistant to tensile strength than shear force.