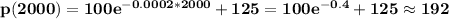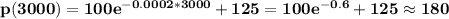Question

The monthly demand for a certain brand of perfume is given by the demand equation p = 100e−0.0002x + 125 where p denotes the retail unit price (in dollars) and x denotes the quantity (in 1-oz bottles) demanded.

(a) Find the rate of change of the price per bottle when x = 2000 and when x = 3000. (Round your answers to four decimal places.)

x = 2000( ) dollars/bottle

x = 3000( ) dollars/bottle

(b) What is the price per bottle when x = 2000? When x = 3000? (Round your answers to the nearest cent.)

x = 2000 $ ( )

x = 3000 $ ( )

Answer 1

a)

Rate of change of the price per bottle when x = 2000

p'(2000)= -0.0134

Rate of change of the price per bottle when x = 3000

p'(3000)= -0.011

b)

Price per bottle when x = 2000

$192

Price per bottle when x = 3000

$180

Explanation:

The equation of the demand x in terms of the price p is

`\bf p(x)=100e^(-0.0002x)+125`

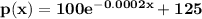
(a) Find the rate of change of the price per bottle when x = 2000 and when x = 3000. (Round your answers to four decimal places.)

These are p'(x) at x=2000 and x=3000

`\bf p'(x)=100(-0.0002)e^(-0.0002x)=-0.02e^(-0.0002x)`

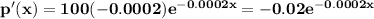
so

`\bf p'(2000)=-0.02e^(-0.0002*2000)=-0.02e^(-0.4)=-0.0134`

`\bf p'(3000)=-0.02e^(-0.0002*3000)=-0.02e^(-0.6)=-0.011`

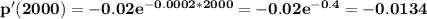
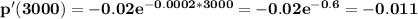
(b) What is the price per bottle when x = 2000? When x = 3000? (Round your answers to the nearest cent.)

These are p(2000) and p(3000)

`\bf p(2000)=100e^(-0.0002*2000)+125=100e^(-0.4)+125\approx 192`

`\bf p(3000)=100e^(-0.0002*3000)+125=100e^(-0.6)+125\approx 180`