Question

A 3 kg block is released from rest to slide down a ramp with friction. The length that the block slides is 2 meters and the angle of the ramp is 30°. The coefficient of kinetic friction between the surface and the block is 0.20. a. List all of the forces on the block. b. Calculate the amount of work done by each force. c. What is the total work done on the block? d. What is the final speed of the block?

Answer 1

(a). The acceleration is 3.20 m/s².

(b). The amount of work done by each force is 19.2 J.

(c). The total work done on the block is 19.2 J.

(d). The final speed of the block is 6.26 m/s.

Step-by-step explanation:

Given that,

Mass of block = 3 kg

Distance = 2 m

Angle = 30°

Coefficient of kinetic friction = 0.20

(a). We need to calculate the acceleration

Using balance equation of force

`N = mg\co\theta`

`mg\sin\theta-f_(k)=ma`

`a = g\sin\theta-\mu g\cos30`

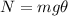
Put the value into the formula

`a=g(\sin30-0.20\cos30)`

`a=9.8((1)/(2)-0.20*(√(3))/(2))`

`a=3.20\ m/s^2`

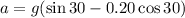
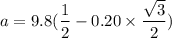
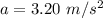
The acceleration is 3.20 m/s².

(b). We need to calculate the amount of work done by each force

Using formula of work done

Normal force is

`N = mg\cos30`

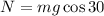
So due to this the net force is zero then the no work done by reaction force.

By another force,

`W= F* d`

`W=ma* d`

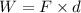
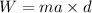
Put the value into the formula

`W= 3*3.20*2`

`W=19.2\ J`

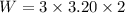
The amount of work done by each force is 19.2 J.

(c). We need to calculate the total work done on the block

The total work done on the block is 19.2 J.

(d). We need to calculate the final speed of the block

Using equation of motion

`v^2=u^2+2gs`

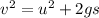
Put the value into the formula

`v^2=0+2*9.8*2`

`v=√(2*9.8*2)`

`v=6.26\ m/s`

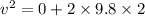
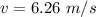
The final speed of the block is 6.26 m/s.

Hence, This is the required solution.