Question

Two 1.50-V batteries with their positive terminals in thesame direction are inserted in

series into the barrel of a flashlight. One battery has an internalresistance of 0.255 Ω , the other
an internal resistance of 0.153 Ω .

When the switch isclosed, a current of 600 mA occurs in the lamp.

(a) What is the lamp’s resistance?

(b) What fraction ofthe chemical energy transformed appears as internal energy in the batteries?

Answer 1

To develop this problem it is necessary to collect the concepts related to Ohm's Law.

Ohm's law can be expressed as:

`V = I*R`

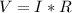
Where

V = Voltage

I = Current

R = Resistance

For our problem the total values of the variables would be given by:

`V = 2(1.5) = 3.0V \rightarrow` Two batteries

`r = (0.255\Omega)+(0.153\Omega)`

`r = 0.408\Omega`

`I = 0.6A`

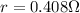
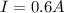
PART A) Whereas the lamp resistance is a surplus greater than the previous resistance given, it must be

`V = I (R+r)`

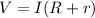
Where R is the resistance of the lamp,

`R = (V)/(I)-r`

`R = (3)/(0.6)-0.408`

`R =4.59\Omega`

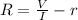
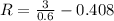
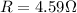
PART B) To calculate the percentage difference in the internal potential we start by calculating the internal voltage given by

`V' = Ir`

`V' = (0.6)(0.408)`

`V' = 0.245V`

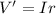
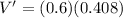
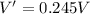
Then the fraction of energy trasnferred is

`(V')/(V) = (0.245)/(3)*100\\(V')/(V) = 8.16\%`

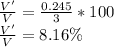
Therefore the fraction of the chemical energy transformed is 8.16%