Question

A horizontal disk rotates about a vertical axis through its center. Point P is midway between the center and the rim of the disk, and point Q is on the rim. If the disk turns with constant angular velocity, which of the following statements about it are true? (There may be more than one correct choice.)

A. P and Q have the same linear acceleration.
B. The angular velocity of Q is twice as great as the angular velocity of P.
C.The linear acceleration of P is twice as great as the linear acceleration of Q.
D. The linear acceleration of Q is twice as great as the linear acceleration of P.
E. is moving twice Q as fast as P.

Answer 1

If the disk turns with constant angular velocity, the following statements about it are true

• The linear acceleration of Q is twice as great as the linear acceleration of P
• is moving twice Q as fast as P.

Answer: Options D and E

Explanation:

Let us consider that R is the radius of the circular disc. So as Q is on the rim, so the distance of Q from the centre of the disc is R and as P is the midpoint between centre and rim of the disk, so the distance of P from the centre is R/2.

As we know that the angular velocity of the circular disk will be equal to the ratio of distance covered by that point to the time taken. So the angular velocity at point Q will be

`\text { Angular velocity at point } Q=\frac{\text { Distance covered by point } Q}{\text { Time }}=(2 \pi R)/(T)=v`

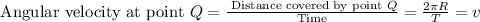
As R is the distance of point Q from the centre of the disc.

Similarly ,

`\text { Angular velocity at point } P=\frac{\text { Distance covered by point } P}{\text { Time }}=\frac{2 \pi\left(\frac{\mathrm{R}}{2}\right)}{T}=(\pi R)/(T)=v^(\prime)`

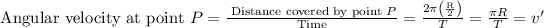
So if we equate v with v’ we obtain that

`v=2 v^(\prime)`

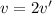
Therefore, the point Q will be moving twice as fast as P. As the velocity of Q is more than O, the linear acceleration of point Q will also be twice as great as the linear acceleration of P.

This is because acceleration is directly proportional to the rate of change in velocity. So if velocity increases in the factor of 2, the acceleration of point Q will also increase twice with respect to point P.