Question

Solve the equation and determine the solution(s) or any extraneous solution.

Answer 1

Solution: x = 9 Extraneous solution: x = 1

Explanation:

Given equation:

`√(4x)=x-3`

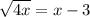
Square both sides:

`\implies \left(√(4x)\right)^2=\left(x-3\right)^2`

`\implies 4x=x^2-6x+9`

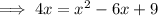
Subtract 4x from both sides:

`\implies 4x-4x=x^2-6x+9-4x`

`\implies 0=x^2-10x+9`

`\implies x^2-10x+9=0`

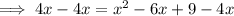
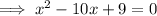
Split the term in x:

`\implies x^2-x-9x+9=0`

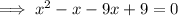
Factor the first two terms and the last two terms separately:

`\implies x(x-1)-9(x-1)=0`

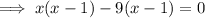
Factor out the common term (x - 1):

`\implies (x-9)(x-1)=0`

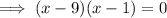
Apply the zero-product property:

`(x-9)=0 \implies x = 9`

`(x-1)=0 \implies x=1`

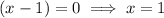
Substitute the found values of x into the original equation to verify the solutions:

`\begin{aligned}x=9 \implies √(4 \cdot 9) & = 9-3\\√(36) & = 6\\6 & = 6\end{aligned}`

`\begin{aligned}x=1 \implies √(4 \cdot 1) & = 1-3\\√(4) & = -2\\ 2 & = -2\end{aligned}`

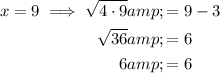
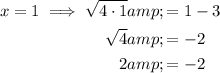
Therefore, the only valid solution is x = 9:

• Solution: x = 9
• Extraneous solution: x = 1

Extraneous solution: A solution from the process of solving the equation that is not a valid solution to the original equation.