Question

Given f(x) and g(x) = k⋅f(x), use the graph to determine the value of k.

Two lines labeled f of x and g of x. Line f of x passes through points negative 4, 0 and negative 3, 1. Line g of x passes through points negative 4, 0 and negative 3.

3
one third
negative one third
−3

Answer 1

-3

Explanation:

Answer 2

Answer: -3.

Explanation:

We are given that :
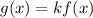`g(x)=kf(x)` (1)

It means that f(x) and g(x) are proportional.

[Equation of direct variation: y=kx , where k= proportionality constant.]

From the given graph ,

At x= -3 , f(x)=1 and g(x) =-3

Put value of x=-3 in (1) , we get

`g(-3)=kf(-3)`

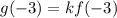
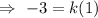`\Rightarrow\ -3=k(1)` [∵ f(x)=1 and g(x) =-3]

`\Rightarrow\ -3=k`

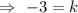
i.e. The value of k = -3

Hence, the correct answer is -3.