Question

Help with these questions please!

Answer 1

9. (1)

10. (2)

11. (3)

12. (2)

Explanation:

9. Given the equation of the parabola

`(y-3)^2=8(x-2)`

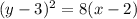
If the equation of the parabola is in form
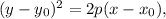`(y-y_0)^2=2p(x-x_0),` then
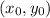`(x_0,y_0)` are the coordinates of its vertex and p is parabola's parameter. So, the vertex is at (2,3) and p = 4.

This parabola goes in positive x-direction, so the focus is at

`F\left((p)/(2)+x_0,y_0\right)\\ \\F(2+2,3)\\ \\ F(4,3)`

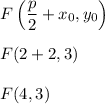
and the equation of the directrix is

`x=-(p)/(2)+x_0\\ \\x=-2+2\\ \\x=0`

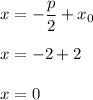
Correct option is (1)

10. The diagram shows the absolute value function with vertex at (3,0). From the graph you can see that the left part of the graph determines increasing function (when going by the graph, you'll go up) and the right part of the graph determines the decreasing function (when going by the graph, you'll go down). So,

• increasing for
  `x\in (-\infty ,3);`
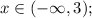
• decreasing for
  `x\in (3,\infty).`

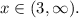
11. Given

`f(x)=x^4+x^2`

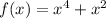
and

`g(x)=-x^3+5`

Definition: Function
`f(x)` is an even function, if for all x from the domain,
`f(-x)=f(x)`

Definition: Function
`f(x)` is an odd function, if for all x from the domain,
`f(-x)=-f(x)`

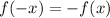
Consider function f(x):

`f(-x)=(-x)^4+(-x)^2=x^4+x^2=f(x)`

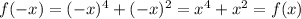
So, the function f(x) is an even function and is not an odd function. Thus, option (3) is false

12. Consider function

`f(x)=-x^2+12x-4`

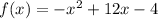
Find the discriminant:

`D=b^2-4ac=12^2-4\cdot (-1)\cdot (-4)=144-16=128`

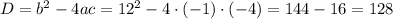
Since the discriminant is greater than 0, the function has 2 different rational roots. These roots are irrational, because
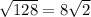`√(128)=8√(2)` is an irrational number.

So, correct option is (2)