Answer:
(a) the temperature of the drink after 45 minutes is 12.77
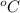
(b) its temperature be 14
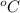 at t = 56.50 Minutes
at t = 56.50 Minutes
Explanation:
Given information:
Initial temperature,
 = 5
= 5
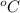
Sorrounding temperature, C = 20
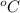
in 25 minute, T(25) = 10
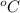
(a) the temperature of the drink after 45 minutes
According Newton's law of cooling
T(t) = C + (
 - C)
- C)

where
 = initial temperature
= initial temperature
t = time
k = cooling constant
C = sorrounding temperature
Thus,
T(25) = 20 + (5 - 20)

10 = 20 - (15
 )
)
 =
=
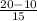
-25k = ln(
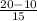 )
)
k = - (ln(
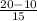 ))/25
))/25
= 0.016
hence, the complete equation
T(t) = 20 + (5 - 20)
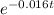
in 45 minute the temperature is
T(45) = 20 + (5 - 20)
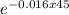
T(45) = 12.77
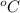
the temperature is 14
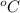 , so T(t) = 14
, so T(t) = 14
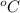
T(t) = 20 + (5 - 20)
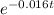
14 = 20 + (5 - 20)
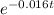
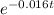 =
=
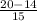
-0.016t = ln (
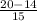 )
)
t = - (ln (
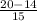 ))/ 0.016)
))/ 0.016)
t = 56.50 Minutes