Question

Write an equation in standard form of the line that passes through the given point and has the given slope m

-4=1/2(-15)+b

Answer 1

The equation in standard form of the line that passes through the given point and has the given slope and
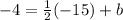`-4=(1)/(2)(-15)+b` is x – 2y = - 7

Solution:

Given that, We have write an equation in standard form of the line that passes through the given point and has the given slope "m"

Given equation is,

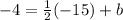`-4=(1)/(2)(-15)+b` ---- eqn 1

Here, if we observe the above given equation it is in the form of the slope – intercept form, i.e. y = mx + c

Where "m" is the slope of line and "c" is the y-intercept

So, now by comparison we get,

`m=(1)/(2), x=-15, y=-4`

Which means that, line is passing through (-15, -4) at a slope of
`(1)/(2)`

Now, solve (1) for intercept,

Plugging in m = 1/2 and (x, y) = (-15, -4) we get,

`\begin{array}{l}{\rightarrow-4=(1)/(2)(-15)+b} \\\\ {\rightarrow-4=(-15)/(2)+b} \\\\ {\rightarrow b=(15)/(2)-4=(15-8)/(2)} \\\\ {\rightarrow b=(7)/(2)}\end{array}`

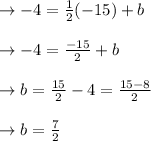
Then, the line equation in slope intercept form will be

`y=(1)/(2) x+(7)/(2)`

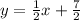
Rearranging the terms to get standard form,

`\rightarrow 2 y=x+7 \rightarrow x-2 y=-7`

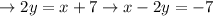
hence, the line equation in standard form is x – 2y = - 7