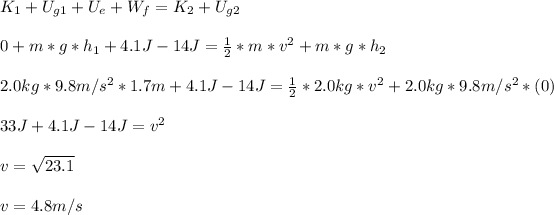Answer:
a) 4.1 J
b) -14 J
c) 4.8 m/s
Step-by-step explanation:
The energy stored in the spring is given by:
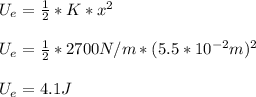
The mechanical energy loss is because of the work done by the friction force.
The friction force (only presented on the inclined surface) is given by:
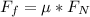
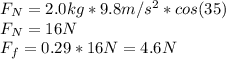
We need to calculate the length of the ramp in order to calculate the work, the length of the ramp is the hypotenuse:
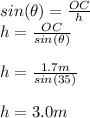
So the work done by the friction force is:
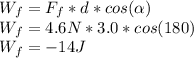
the angle is 180 degrees because the force is opposite to the motion.
In order the know the final velocity we need to apply the Energy Conservation Theorem: