Question

A 16.5-kg crate starts at rest at the top of a 60.0° incline. The coefficients of friction are μs = 0.400 and μk = 0.300. The crate is connected to a hanging 8.00-kg box by an ideal rope and pulley. How long does it take the crate to slide 2.00 m down the incline?

Answer 1

t = 1.62 s

Step-by-step explanation:

given,

mass of the block m₁ = 16.5 Kg

m₂ = 8 Kg

angle of inclination = 60°

μs = 0.400 and μk = 0.300

time to slide 2 m = ?

a) let a is the acceleration of the block m₁ downward.

Net force acting on m₂,

F₂ = T - m₂ g

m₂a = T - m₂ g

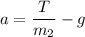`a = (T)/(m_2) - g`.......(1)

net force acting on m₁

F₁ = m₁g sin(60°) - μ_k m₁g cos (60°) - T

m₁ a = m₁g sin(60°) - μ_k m₁g cos (60°) - T

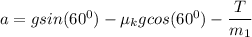`a = g sin(60^0) - \mu_k g cos (60^0) - (T)/(m_1)`.........(2)

from equations 1 and 2

`(T)/(m_2) - g = g sin(60^0) - \mu_k g cos (60^0) - (T)/(m_1)`

`(T)/(m_2) +(T)/(m_1) = g+ g sin(60^0) - \mu_k g cos (60^0)`

`T(m_1+m_2)/(m_2* m_1) = g+ g sin(60^0) - \mu_k g cos (60^0)`

`T = (g+ g sin(60^0) - \mu_k g cos (60^0))/((m_1+m_2)/(m_2* m_1))`

`T = {m_2* m_1}\frac{g+ g sin(60^0) - \mu_k g cos (60^0)}{{m_1+m_2}}`

`T = {16.5* 8}\frac{9.8 + 9.8 sin(60^0) - 0.3* 9.8 cos (60^0)}{{16.5+8}}`

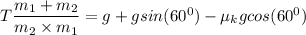
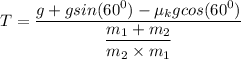
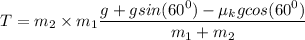
T = 90.61 N

from equation (1)

`a = (90.61)/(8) - 9.8`.......(1)

a = 1.52 m/s²

let t is the time taken

Apply,

d = ut + 0.5 a t²

2 = 0 + 0.5 x 1.52 x t²

`t = √(2.63)`

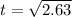
t = 1.62 s