Question

Computech Corporation is expanding rapidly and currently needs to retain all of its earnings; hence, it does not pay dividends. However, investors expect Computech to begin paying dividends, beginning with a dividend of $0.50 coming 3 years from today. The dividend should grow rapidly - at a rate of 28% per year - during Years 4 and 5, but after Year 5, growth should be a constant 8% per year. If the required return on Computech is 18%, what is the value of the stock today? Do not round intermediate calculations. Round your answer to the nearest cent.

Answer 1

The value of the stock today is $4.86

Step-by-step explanation:

Hi, first we need to find the value of dividend 4, 5 and 6, ths las one we will use to find the perpetuity value of this stock (since it will grow at 8% from year 5). So, let´s go ahead and find D4, D5 and D6

`D4=0.50*(1+0.28)=0.64\\D5=0.64*(1+0.28)=0.8192\\D6=0.8192*(1+0.28)=0.884736`

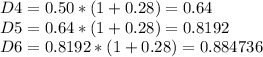
Now, we need to find the price of this stock, for that we have to bring to present value all those cash flows.

`Price=(D3)/((1+0.18)^(3) ) +(D4)/((1+0.18)^(4) ) +(D5)/((1+0.18)^(5) ) +(D6)/((r-g)) ((1)/((1+0.18)^(5) ) )`

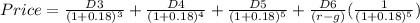
Where:

r = required return of Computech

g= growth rate from year 5 (8%)

Everything should look like this.

`Price=(0.5)/((1+0.18)^(3) ) +(0.64)/((1+0.18)^(4) ) +(0.8192)/((1+0.18)^(5) ) +(0.884736)/((0.18-0.08)) ((1)/((1+0.18)^(5) ) )`

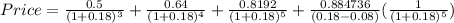
Therefore:

`Price= 4.86`

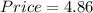
So, today´s value of this stock is $4.86