Question

The length of an intercepted arc of a central angle of a circle is 4 cm. If the radius of the circle is 5 cm, what is the measurement of the central angle to the nearest whole degree?

Answer 1

46°

Explanation:

Lets use the formula for arc length (in radian). Then we will convert radians to degrees.

`s=r\theta`

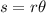
Where

s is the length of intercepted arc

r is the radius

`\theta` is the angle in radians

Given,

s = 4

r = 5

We find
`\theta`:

`s=r\theta\\4 = 5\theta\\\theta =(4)/(5)=0.8`

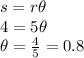
So, central angle = 0.8 radians

To convert from radians to degrees, we use the conversions ratio shown below:

`\pi Radians = 180Degrees`

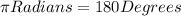
So,

`0.8Radians*(180Degrees)/(\pi Radians)=(0.8*180)/(\pi)=45.84`

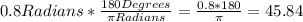
To the nearest degree, we round up to 46°