Question

A credit card had an APR of 33.01% all of last year and compounded interest

daily. What was the credit card's effective interest rate last year?

O A. 37.33%

B. 38.49%

O

c. 35.73%

O

D. 39.09%

Answer 1

Option D - 39.09%

Explanation:

Given : A credit card had an APR of 33.01% all of last year and compounded interest daily.

To find : What was the credit card's effective interest rate last year?

Solution :

Effective annual rate formula is given by,

`\text{APR}=(1+(r)/(n))^n-1`

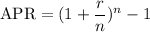
where, r is the interest rate i.e. r=33.01%=0.3301

n is the number of time period for which interest is compounded daily i.e. n=365.

Substitute in the formula,

`\text{APR}=(1+(0.3301)/(365))^(365)-1`

`\text{APR}=(1+000904)^(365)-1`

`\text{APR}=(1.000904)^(365)-1`

`\text{APR}=1.39089-1`

`\text{APR}=0.39089`

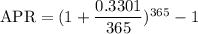
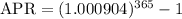
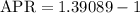
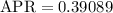
Into percentage,

`\text{APR}=0.39089* 100`

`\text{APR}=39.089\%`

`\text{APR}\approx 39.09\%`

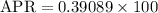
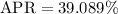
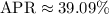
Therefore, the credit card's effective interest rate last year is 39.09%.

So, Option D is correct.