Question

How to find a polynomial function with given zeros with imaginary numbers

Answer 1

To find a polynomial function with given zeros that have imaginary numbers, use the complex conjugate theorem to form the polynomial by multiplying the binomials of each conjugate.

Step-by-step explanation:

To find a polynomial function with given zeros that have imaginary numbers, we need to use the complex conjugate theorem. This theorem states that if a complex number, a + bi, is a zero of a polynomial with real coefficients, then its conjugate, a - bi, is also a zero of that polynomial.

For example, if we have the zeros 2 + 3i and 2 - 3i, we can find the polynomial function by multiplying the binomials (x - (2 + 3i))(x - (2 - 3i)). Expanding this expression gives us a quadratic polynomial function.

So, to find a polynomial function with given zeros that have imaginary numbers, we need to identify the complex conjugates of the zeros and form the polynomial function by multiplying the binomials for each conjugate.

Answer 2

Step-by-step explanation:

First, recall that if α if a root of the polynomial, let's call it P, then (X - α) is a factor of P. If α and β are different roots, then both (X-α) and (X-β) are factors of P and the product, (X-α)*(X-β) = X² - (α+β)*X+ αβ is a factor of P.

I will assume that P has real coefficients. If that is the case, then if w = a + b*i is a root, then its conjugate
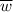`\overline{w}` is also a root of P. Even more,
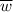`\overline{w}` has the same multiplicity than w.

Take into account this two properties of comlex numbers:

• 
  `w * \overline{w} = |w|^2`
• 
  `w + \overline{w} = 2*re(w)`

where re(w) represents the real part of w. Using this properties we have that the product of the factors

`(X - w) * (X - \overline{w}) = X^2 - 2*re(w) + |w|^2`

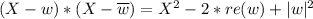
Which is a real coefficient polynomial, because re(w) and |w| are real numbers.

Example

Lets assume that out polynomial P has grade 4, P(0) = 5 and we know 2+i is a double root (root with multiplicity 2). Then its conjugate 2-i is also a root with double multiplicity. We also know that re(2+i) = 2 and |2+i| = √(2²+1²) = √5 Therefore the polynomial

(X- (2+i))² * (X-(2-i))² = X² -4 X + √5

is a factor of P.

Since P has grade four, we can conclude that X² -4 X + √5 differs from P by multiplying by a constant c such that P(X) = c*(X² -4 x + √5)

Note that for hypothesis P(0) = 5, so we have that P(0) = c*(0² - 4*0 +√5) = c*√5. We conclude that c = √5 and hence P(X) = √5*X² - 4*√5 X + 5

Multiplying the factor for its conjugate is the main trick to handle ploynomials with complex roots. After you did that, you can continue as you did with polynomial with real roots.

I hope this helped you!