Question

21​% of adults would pay more for environmentally friendly products. You randomly select 10 adults. Find the probability that the number of adults who would pay more for environmentally friendly products is​ (a) exactly​ two, (b) more than​ two, and​ (c) between two and​ five, inclusive.

Answer 1

Answer: a) 0.3011

b) 0.3526

c) 0.6455

Explanation:

Given : The proportion of adults would pay more for environmentally friendly products : p= 0.21

Sample size : n= 10

Let x be a binomial variable that denotes the number of adults would pay more for environmentally friendly products.

Using binomial distribution,
`P(x)=^nC_xp^x(1-p)^(n-x)`

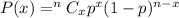
a) The probability that the number of adults who would pay more for environmentally friendly products is exactly 2 will be :-

`P(x=2)=^(10)C_2(0.21)^2(1-0.21)^(10-2)\\\\=(10!)/(2!(10-2)!)(0.21)^2(0.79)^8\approx0.3011`

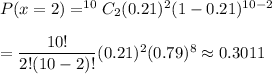
The probability that the number of adults who would pay more for environmentally friendly products is exactly 2=0.3011

b) The probability that the number of adults who would pay more for environmentally friendly products is more than​ two will be :-

`P(x>2)=1-P(x\leq2)=1-(P(x=0)+P(x=1)+P(x=2))\\\\=1-(^(10)C_0(0.21)^0(1-0.21)^(10)+^(10)C_1(0.21)^1(1-0.21)^(9)+0.3011)\\\\=1-((0.79)^(10)+(10)(0.21)(0.79)^9+0.3011)\\\\=1-(0.0946+0.2517+0.3011)\\\\=1-0.6474=0.3526`

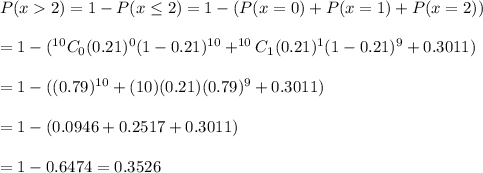
The probability that the number of adults who would pay more for environmentally friendly products is more than​ two =0.3526

c) The probability that the number of adults who would pay more for environmentally friendly products is between two and​ five, inclusive will be :-

`P(2\leq x\leq5)=P(x=2)+P(x=3)+P(x=4)+P(x=5)\\\\=0.3011+^(10)C_3(0.21)^3(1-0.21)^7}+^(10)C_4(0.21)^4(1-0.21)^(6)+^(10)C_5(0.21)^5(1-0.21)^(5))\\\\=0.3011+(10!)/(3!7!)(0.21)^3(0.79)^7+(10!)/(4!6!)(0.21)^4(0.79)^6+(10!)/(5!5!)(0.21)^5(0.79)^5\\\\=0.3011+0.2134+0.0993+0.0317=0.6455`

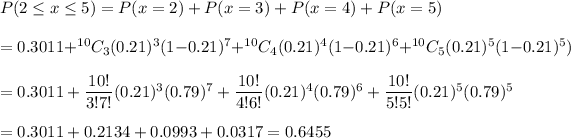
The probability that the number of adults who would pay more for environmentally friendly products is between two and​ five, inclusive =0.6455