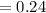Answer:
It is
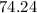 degrees Fahrenheit when the crickets are chirping
degrees Fahrenheit when the crickets are chirping
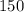 times a minute.
times a minute.
Variables
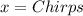 and
and
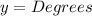
y-intercept
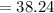
slope
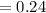
Explanation:
As the chirps are
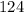 times per minute for
times per minute for
 degrees Fahrenheit we will consider it in
degrees Fahrenheit we will consider it in
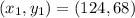 .
.
Now when the chirps are
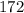 times and temperature is
times and temperature is
 degrees we consider it
degrees we consider it
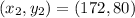 .
.
To find the slope we can use point-slope formula.
Where
 is the slope and
is the slope and
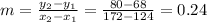
To find y-intercept we will plug out the value of slope in
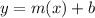 choosing point
choosing point
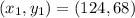 .
.
So
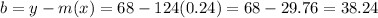
And the equation is
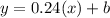
To calculate temperature for
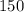 chirpings we have to plug
chirpings we have to plug
 and
and
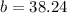 in our above equation which is in form of
in our above equation which is in form of
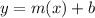
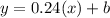
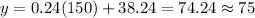 degrees Fahrenheit.
degrees Fahrenheit.
Finally we have :
Temperature
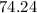 degrees Fahrenheit.
degrees Fahrenheit.
With variables
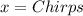 and
and
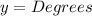
y-intercept
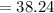 and
and
slope