Answer:
(a) 0.8655
(b)0.8655
Explanation:
X is the number of respodents who agree
P(x ≥4), n=12, p=0.45
P(x ≥4)=1-P(x<4)
P(x<4)=P(0 ≤x<4)= P(0 ≤x≤3)=P(x=0,1,2,3)=P(x=0)+P(x=1)+P(x=2)+P(x=3)
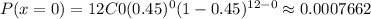
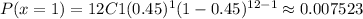
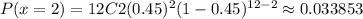
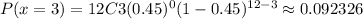
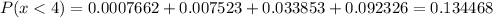
P(x ≥4)=1-P(x<4)=1-0.134468=0.8655319
(b)
Y represent those who agree
P(Y≤8), n=12, p=0.45
P(Y≤8)=1-P(Y>8)
P(Y>8)=P(8<Y≤12)=P(9≤Y≤12)=P(Y=9,10,11,12)
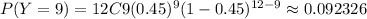
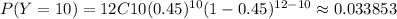
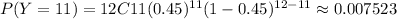
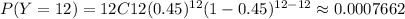
Total =0.134468
P=1-0.134468=0.8655319