Question

Please help me with this question I'm so confused

Answer 1

x = 15

Explanation:

Since the triangles are similar that means that the sides are proportional. There are a couple of ways to find x. One way is to find the scale factor. We can use the two corresponding sides that we know. 25 and 10 are corresponding sides. They are both the hypotenuse of their triangles or you can say that they are both the side across from the 90 degree angle.

There is some number that I can multiple 10 by to get 25. This is my scale factor. This is how I can find it.

Let s = the scale factor.

10s = 25 Divide both sides of the equation by 10

s = 2.5 This means that each side of the larger triangle is 2.5 times longer than each side of the original triangle.

To find x. Find is corresponding side on the right and take that length and multiple it by 2.5

6 x 2.5 = 15

Another way is to set up a proportion.

`(10)/(6)` =
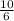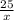`(25)/(x)` I could cross multiply and solve for x

10x = (6)(25)

10x = 150 Divide both sides by 10

x = 15

Answer 2

x is equal to 15.

Explanation:

In this problem, it is said that ΔABC ~ ΔXYZ. This means that the shapes are the same, however they are not the same size. Here the problem is asking for the value of x when the triangle is scaled up.

Look on the triangles for where there are values on both ABC and XYZ. Notice that the hypotenuse for both triangles have a value.

The hypotenuse of triangle XYZ is 10, while the hypotenuse of triangle ABC is 25. Dividing both of those results by 10 results in a 1:2.5 ratio, meaning that the values of triangle ABC are 2.5 times larger than the values of triangle XYZ.

Knowing this, take the value of XZ on triangle XYZ, and multiply it by 2.5 to get the value of AC on triangle ABC, or x.

6 * 2.5 = 15

The value of x is 15.