Answer:
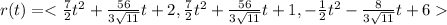
Explanation:
We are given that
Initial position of particle =
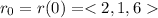
Initial speed of the particle = 8 m/s
Acceleration=7 i+7j-k=<7,7,-1>
We have to find the equation of position vector r(t) of the particle at time t.
We know that
Acceleration=a=
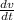
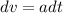
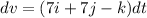
Integrating on both sides then, we get
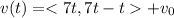
Where
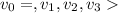
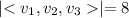
Since, the particle travel in straight line to (9,8,5) and (9,8,5)-(2,1,6)=<7,7,-1>
There exist a constant s such that

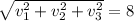
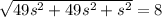
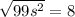
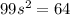
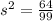
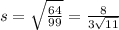
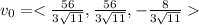
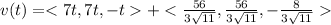
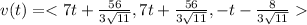

Integrating on both sides then we get

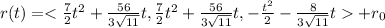
Where
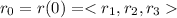 =Some constant vector
=Some constant vector
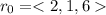
Substitute the value
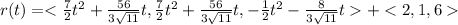
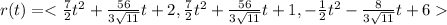
This is required equation of the position vector r(t) of the particle at time t.