Question

Write a system of two equations that can be used to answer this question. A sum of money amounting to $3.70 consists of dimes and quarters. If there are 19 coins in all, how many are quarters?

Answer 1

12

Explanation:

Answer 2

Number of quarters = 12

Explanation:

Let number of dimes be =
`d`

Let number of quarters be =
`q`

Total number of coins =19

Therefor the first equation would be :

`d+q=19`

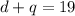
Total sum of money = $3.70 =
`3.70*100 \ cents= 370 \ cents`

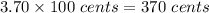
Value of 1 dime = 10 cents

Therefore value of
`d` dimes =
`d* 10=10d` cents

Value of 1 quarter = 25 cents

Value of
`q` quarters =
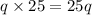`q* 25= 25q` cents

Total value of coins =
`10d+25q`

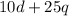
Therefore the 2nd equation would be:

`10d+25q=370`

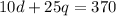
So the system can be written as :

`d+q=19\\10d+25q=370`

We can solve the system using substitution method:

Taking equation 1

`d+q=19\\`

Subtracting both sides by
`q`

`d+q-q=19-q\\d=19-q`

Substitution the value of
`d` in equation 2.

`10(19-q)+25q=370`

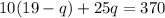
Now, we need to solve for
`q`

Using distribution.

`(10* 19)-(10* q)+25 q=370\\190-10q+25q=370\\`

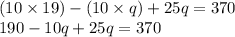
Combining like terms.
`190+15q=370`

Subtracting both sides by 190.

`190-190+15q=370-190\\15q=180`

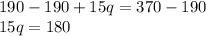
Dividing both sides by 15.

`(15)/(15)q=(180)/(15)\\\\q=12`

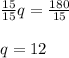
Therefore number of quarters = 12