Question

You are on the roof of a building, 46.0 m above the ground. Your friend, who is 1.80 m tall, is standing next to the building. What speed would an egg dropped from rest be traveling when it hit your friend on the top of his head?

Answer 1

The speed of egg is 14.73 m/s

Step-by-step explanation:

Given the height of building (H) = 46 m

The height of friend (h) = 1.8 m

Distance for the egg to travel (s) = H – h = 46 – 1.8 = 44.2 m

Applying second equation of motion,

`s=u t+(1)/(2) g t^(2)`

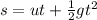
u = 0 (as the egg is starting from the rest)

g = 9.81
`m/s^2`(as the object is falling)

Substituting the values,

44.2=0+
`(1)/(2) *9.81 * t^(2)`

`t^(2)=(44.2 * 2)/(9.81)`

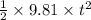
`t^2` = 9

t = 3 sec

Calculating speed,

Speed =
`\frac{\text { Distance }}{\text { time }}`

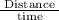
Speed =
`(44.2)/(3)=14.73 \mathrm{m} / \mathrm{s}`

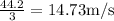
Therefore, the speed of egg is 14.73 m/s

Answer 2

29.448
`ms^(-1)`

Step-by-step explanation:

first determine the distance from the top of the roof to the friends head.

Since he is 1.80 min height ,

distance = 46.0-1.80

= 44.2 m

egg is dropped from rest means that its starting velocity is zero. It has to travel 44.2 m subjected to the gravitational acceleration

Applying Motion equation

`v^(2)=u^(2)+2as`

where v= end velocity (speed)

u=Starting velocity

a= acceleration

s= Distance

(Let gravitational acceleration assumed as
`9.81 ms^(-2)`

`v^(2) =0^(2) +2*9.81*44.2\\v^(2) =867.204\\v=√(867.204)  \\v=29.448  ms^(-1)`