Question

Two points A and B lie on opposite sides of a river. Another point C is located on the same side of the river as B at a distance of 240 ft from B. If angle ABC is 100° and angle ACB is 25°, find the distance across the river from A to B. (Round your answer to two decimal places.)

Answer 1

128.98 feet

Explanation:

By the given information,

Suppose ABC is a triangle,

According to the question,

BC = 240 feet,

m∠ABC = 100°,

m∠ACB = 25°,

∵ m∠ACB + m∠ABC + m∠BAC = 180°,

25° + 100° + m∠BAC = 180°,

125° + m∠BAC = 180°,

⇒ m∠BAC = 55°,

Now the law of sine,

`(\sin C)/(AB)=(\sin A)/(BC)`

`(\sin 25^(\circ))/(AB)=(\sin 55^(\circ))/(240)`

`\implies AB = (250 \sin 25^(\circ))/(\sin 55^(\circ))\approx 128.98`

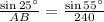
Hence, the distance between A and B would be 128.98 ft ( approx )