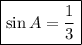Question

I need help on the attached problem ASAP!

Answer 1

`\displaystyle \sin A=(1)/(3)`

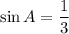
Explanation:

Trigonometric Ratios

The ratios of the sides of a right triangle are called trigonometric ratios. The longest side of the triangle is called the hypotenuse and the other two sides are called the legs.

We are given a triangle with side lengths of 3,
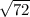`√(72)`, and 9, where 9 is the hypotenuse. Before applying the trigonometric ratios, we must check if the triangle is right, and the Pythagora's theorem is satisfied:

`9^2=3^2+(√(72))^2`

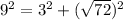
81=9+72=81

Now we're sure it's a right triangle, we apply the sine formula:

`\displaystyle \sin A=\frac{\text{opposite leg}}{\text{hypotenuse}}`

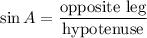
The opposite leg to A is 3, and the hypotenuse is 9, then:

`\displaystyle \sin A=(3)/(9)`

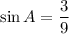
Simplifying:

`\boxed{\displaystyle \sin A=(1)/(3)}`