Question

Thirty-five small communities in Connecticut (population near 10,000 each) gave an average of x = 138.5 reported cases of larceny per year. Assume that σ is known to be 42.7 cases per year.

(a) Find a 90% confidence interval for the population mean annual number of reported larceny cases in such communities. What is the margin of error? (Round your answers to one decimal place.)
(b) Find a 95% confidence interval for the population mean annual number of reported larceny cases in such communities. What is the margin of error? (Round your answers to one decimal place.)
(c) Find a 99% confidence interval for the population mean annual number of reported larceny cases in such communities. What is the margin of error? (Round your answers to one decimal place.)

Answer 1

Part A:

Error Margin= 11.9

Interval is 126.6 to 150.4

Part B:

Error Margin=14.1

Interval is 124.4 to 152.6

Part C:

Error Margin=18.6

Interval is 119.9 to 157.1

Explanation:

Confidence Interval Z

90% 1.645

95% 1.96

99% 2.58

Formula used in all three parts:

Error Margin=Z*σ/
`√(n)`

Upper limit of Interval=x+ Error Margin

Lower limit of Interval=x- Error Margin

Part A:

Error Margin=1.645*42.7/
`√(35)`

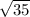
Error Margin= 11.9

Upper limit of Interval=138.5+ 11.9

Upper limit of Interval=150.4

Lower limit of Interval=138.5 - 11.9

Lower limit of Interval=126.6

Interval is 126.6 to 150.4

Part B:

Error Margin=1.96*42.7/
`√(35)`

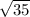
Error Margin=14.1

Upper limit of Interval=138.5+ 14.1

Upper limit of Interval=152.6

Lower limit of Interval=138.5 - 14.1

Lower limit of Interval=124.4

Interval is 124.4 to 152.6

Part C:

Error Margin=2.58*42.7/
`√(35)`

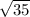
Error Margin=18.6

Upper limit of Interval=138.5+ 18.6

Upper limit of Interval=157.1

Lower limit of Interval=138.5 - 18.6

Lower limit of Interval=119.9

Interval is 119.9 to 157.1