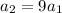Question

A car turns a corner at 5 mph. If its speed is increased to 15 mph, its centripetal acceleration is:

Answer 1

Centripetal acceleration, property of the motion of a body traversing a circular path. The acceleration is directed radially toward the centre of the circle and has a magnitude equal to the square of the body's speed along the curve divided by the distance from the centre of the circle to the moving body.

Answer 2

The centripetal acceleration becomes 9 times to that of initial acceleration.

Explanation:

It is clear that the car is in circular motion. While possessing circular motion, any object undergoes centripetal acceleration. This centripetal acceleration is always directed towards the centre.

And due to this force itself, a body can rotate, otherwise, it will move away into the centre. The centripetal acceleration depends upon the magnitude of the velocity of the car with which it is running. Hence, let us take two instances.

Instance 1,

Velocity of the car 1,
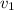`v_(1)` = 5 mph.

Instance 2,

Velocity of the car 2,
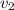`v_(2)` = 15 mph

`a_(c)=(v^(2))/(r)`

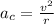
Now, solving by dividing equation for both instances using the above mentioned formula,

`(a_(1))/(a_(2))=(v_(1)^(2))/(v_(2)^(2))`

then, after simplification, we get

`a_(2)=a_(1) * (v_(2)^(2))/(v_(1)^(2))=a_(1) * (15^(2))/(5^(2))`

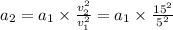
And, hence,

`a_(2)=9 a_(1)`