Question

If 45% of cars are traveling in excess of 70mph, and 8 random cars are measured via radar: what is the probability that at least 1 car is going over 70mph

Answer 1

The required probability is 0.9916

Explanation:

Consider the provided information.

If 45% of cars are traveling in excess of 70mph,

Therefore, p = 0.45

q = 1-p = 1-0.45 = 0.55

8 random cars are measured via radar: n = 8

We need to find at least 1 car is going over 70mph.

According to binomial distribution:
`P(X=x)=^nC_rp^rq^(n-r)`

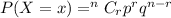
We need to find P(X≥1)

`P(X\geq 1)=1-P(X=0)`

`P(X\geq 1)=1-^8C_0(0.45)^0(0.55)^(8-0)`

`P(X\geq 1)=1-(0.55)^(8)`

`P(X\geq 1)=1-0.0084`

`P(X\geq 1)=0.9916`

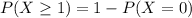
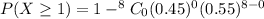
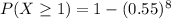
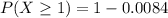
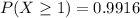
Hence, the required probability is 0.9916