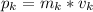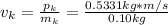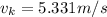Question

A dinner plate falls vertically to the floor and breaks up into three pieces, which slide horizontally along the floor. Immediately after the impact, a 200-g piece moves along the +x-axis with a speed of 2.00 m/s, a 235-g piece moves along the +y-axis with a speed of 1.50 m/s. The third piece has a mass of 100 g. What is the speed of the third piece?

a) 2.51 m/s
b) 5.33 m/s
c) 6.83 m/s
d) 2.57 m/s
e) 3.50 m/s

Answer 1

p_k=\sqrt{p_x^2+p_y^2}}

Step-by-step explanation:

Apply the momentum in each direction knowing that the impact is at the same time for the pieces so

`p_x=m_1*v_1`

`p_x=200g*2.0m/s=0.4kgm/s`

`p_y=m_2*v_2`

`p_y=235g*1.5m/s=0.3525kgm/s`

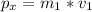
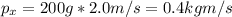
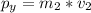
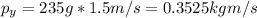
So the momentum in the other piece can be find knowing that

`p_x^2+p_y^2=p_k^2`

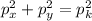
So:

`p_k=√(p_x^2+p_y^2)}`

`p_k=√(0.4^2+0.3525^2)}=√(0.2842 kg^2*m^2/s^2)`

`p_k=0.5331kg*m/s`

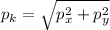
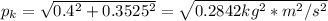
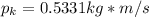
To find the velocity knowing the mass

`p_k=m_k*v_k`

`v_k=(p_k)/(m_k)=(0.5331 kg*m/s)/(0.10kg)`

`v_k=5.331 m/s`