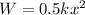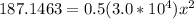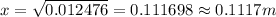Answer:
0.1117 m
Step-by-step explanation:
Given information
m=12 kg, d=3m ,
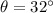 ,
,
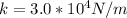
Net work done W = Fd = mgdcos(90-32) and taking g as 9.81
W = 12*9.81*3*sin(32) = 187.1463 J
From the principal of conservation of energy
W = change in potential energy of spring