The additive inverse of a number x is a number y such that

From this definition, we can derive
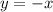
So, to get the additive inverse of a number, you simply have to switch its signs.
Since complex numbers are made of two pieces (real and complex parts), you'll have to switch both signs:

In fact, if you try to sum them, you have
