Question

The coordinates of a particle in the metric​ xy-plane are differentiable functions of time t with StartFraction dx Over dt EndFraction equalsnegative 6 StartFraction m Over sec EndFraction and StartFraction dy Over dt EndFraction equalsnegative 4 StartFraction m Over sec EndFraction . How fast is the​ particle's distance from the origin changing as it passes through the point ​(12​,5​)?

Answer 1

`(dD)/(dt)=-7.076\ m/s`

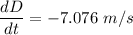
Step-by-step explanation:

It is given that,

The coordinates of a particle in the metric​ xy-plane are differentiable functions of time t are given by :

`(dx)/(dt)=-6\ m/s`

`(dy)/(dt)=-4\ m/s`

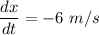
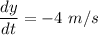
Let D is the distance from the origin. It is given by :

`D^2=x^2+y^2`

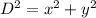
Differentiate above equation wrt t as:

`2D(dD)/(dt)=2x(dx)/(dt)+2y(dy)/(dt)`

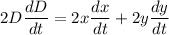
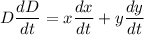`D(dD)/(dt)=x(dx)/(dt)+y(dy)/(dt)`.............(1)

The points are given as, (12,5). Calculating D from these points as :

`D=√(12^2+5^2) =13\ m`

Put all values in equation (1) as :

`13* (dD)/(dt)=12* (-6)+5* (-4)`

`(dD)/(dt)=-7.076\ m/s`

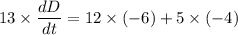
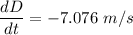
So, the particle is moving away from the origin at the rate of 7.076 m/s. Hence, this is the required solution.