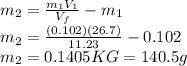To develop the problem, we require the values concerning the conservation of momentum, specifically as given for collisions.
By definition the conservation of momentum tells us that,
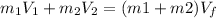
To find the speed at which the arrow impacts the apple we turn to the equation of time, in which,

The linear velocity of an object is given by
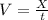
Replacing the equation of time we have to,
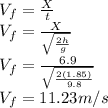
Velocity two is neglected since there is no velocity of said target before the collision, thus,
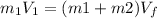
Clearing for m_2