Question

Find a quadratic function with roots x = 7 and x = -1.

Answer 1

The quadratic function with roots x = 7 and x = -1 is
`x^(2)-6 x-7=0`

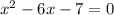
Solution:

Given that , roots of a quadratic equation are x = 7 and x = - 1 .

We have to find the equation of that quadratic function.

Now, we know that, quadratic equation is given by
`x^(2)-(a+b) x+a b=0`

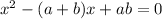
where a and b are roots of that quadratic equation

Here a = 7 and b = -1

By substituting the values in general equation, we get

`\begin{array}{l}{x^(2)-(7+(-1)) x+7(-1)=0} \\\\ {x^(2)-(7-1) x-7=0} \\\\ {x^(2)-(6) x-7=0} \\\\ {x^(2)-6 x-7=0}\end{array}`

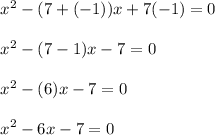
Thus the required quadratic function is found

Answer 2

x^2 - 6x - 7

Explanation:

Roots, 7 and -1

x = 7 is the same as x - 7 = 0

x = -1 is the same as x + 1 = 0

multiply (x-7) by (x + 1)

x(x -7) +1(x - 7)

x^2 -7x + x - 7

x^2 - 6x - 7