Question

Specifications call for the wall thickness of two-liter polycarbonate bottles to average 4.0 mils. A quality control engineer samples 7 two-liter polycarbonate bottles from a large batch and measures the wall thickness (in mils) in each. The results are: 3.999, 4.037, 4.116, 4.063, 3.969, 3.955, and 4.091. It is desired to test H0 : μ = 4.0 versus H1 : μ ≠ 4.0.Make a dotplot of the seven value.

Answer 1

The null hypothesis μ=4.0 could not be rejected.

Explanation:

In this problem we have to perform a hypothesis test of the mean, with s.d. of the population unknown.

The sample is: [3.999, 4.037, 4.116, 4.063, 3.969, 3.955, 4.091]

This sample has a mean of 4.033 and a standard deviation of 0.061.

The null and alternative hypothesis are:

`H_0: \mu = 4.0\\\\H_1: \mu \\eq 4.0`

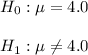
We assume a significance level of 0.05.

The test statistic for this test is:

`t=(M-\mu)/(\sigma)=(4.033-4.0)/(0.061)=0.536`

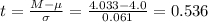
We have a sample size n=7, so the degrees of freedom are 7-1=6.

For a two-tailed test, t=0.536 and df=6, the P-value can be look up in a t-table.

The P-value is 0.61. Is greater than the significance level, so the effect is not significant and the null hypothesis can't be rejected.