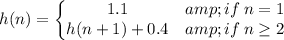Answer:
Part A
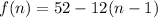
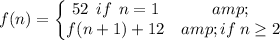
Part B
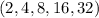 Geometric Sequence
Geometric Sequence
Part C
1/4,3/4,5/4,7/4,9/4
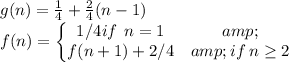
Part D:
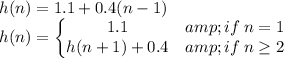
Explanation:
By definition, an Arithmetic Sequence holds the same difference between each following number.
Part A
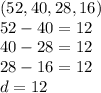
Explicit Formula
To write an explicit formula is to write it as function.
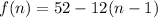
Recursive Formula
To write it as recursive formula, is to write it as recurrence given to some restrictions:
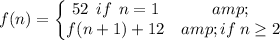
Part B
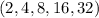
Geometric Sequence, since 2*2=4 8*2=16 and 16*2=32 and 8+2=10 8+16=24
Part C
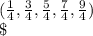
Arithmetic Sequence, difference
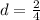
Explicit Formula:
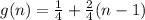
Recursive Formula
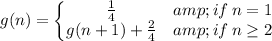
Part D
(1.1,1.5,1.9,2.3,2.7) Arithmetic Sequence, difference d=0.4
Explicit formula
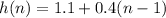
Recursive Formula