Question

A boat moves through the water with two forces acting on it. One is a 2.96×10^3 N forward push by the motor, and the other is a 1.86×10^3 N resistive force due to the water. What is the acceleration of the 1117 kg boat? Answer in units of m/s^2.

The acceleration is 0.98478066248881

If it starts from rest, how far will it move in
17.9 s?
Answer in units of m.

It will move 157.76678603402

What will be its speed at the end of this time
interval?
Answer in units of m/s
I Need Help Here

Answer 1

(a)
`0.984781 m/s^(2)`

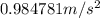
(b) 157.76679 m

(c) 17.62757 m/s

Step-by-step explanation:

Net force acting,
`F_(net)=2.96*10^(3)-1.86*10^(3)=1.1*10^(3)N`

Acceleration,
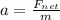`a=\frac {F_(net)}{m}` where m is the mass

`a=\frac {1.1*10^(3)}{1117}= 0.984781 m/s^(2)`

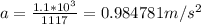
(b)

From kinematic equation

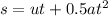`s=ut+0.5at^(2)` where s is displacement, u is initial velocity, t is time taken and a is acceleration.

Considering that u=0 since it starts at rest

`s=0.5at^(2)` and substituting the value of a as calculated in part a, t is 17.9 s hence

`s=0.5*0.984781*17.9^(2)=157.76679 m`

(c )

From kinematic equation

v=u+at where u and v are initial and final velocities respectively, a is acceleration and t is duration in seconds. Since it starts from rest, u=0 and substituting the value of a as found in part a, t given as 17.9 s we get

V=0+0.984781*17.9=17.62757 m/s