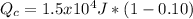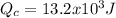Answer:
a).
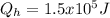
b).
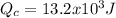
Step-by-step explanation:
a).
Using the law of thermodynamic and using to isovolumetric
ΔU=Qh
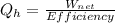
So to determine the internal energy knowing the work it do
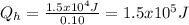
b).
Efficiency is the work done in relation of the work apply in this case to produce heat so:
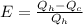
Solve to Qc
![Q_(c)=Q_(h)*[1-E]](https://img.qammunity.org/2020/formulas/physics/high-school/68wvzi03k7q6mcozvztmwqse26lnup0k65.png)