Question

The diameters of Douglas firs grown at a Christmas Tree Farm are normally distributed with a mean of 4 inches and a standard deviation of 1.5 inches. What proportion of the trees are expected to have diameters greater than 5 inches? Group of answer choices

Answer 1

The proportion of trees greater than 5 inches is expected to be 0.25 of the total amount of trees.

Explanation:

In this problem we have a normal ditribution with mean of 4.0 in and standard deviation of 1.5 in.

The proportion of the trees that are expected to have diameters greater than 5 inches is equal to the probability of having a tree greater than 5 inches.

We can calculate the z value for x=5 in and then look up in a standard normal distribution table the probability of z.

`z=(x-\mu)/(\sigma)=(5-4)/(1.5)=0.67`

`P(x>5)=P(z>0.67)=0.25`

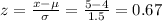
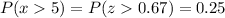
The proportion of trees greater than 5 inches is expected to be 0.25 of the total amount of trees.