Question

You take the same 3 kg metal block and slide it along the floor, where the coefficient of friction is only 0.4. You release the block with an initial velocity of 6 m/s. How long will it take for the block to come to stop? How far does the block move?

Answer 1

1.52905 seconds

4.58715 m

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

`\mu` = Coefficient of friction = 0.4

g = Acceleration due to gravity = 9.81 m/s²

a = Acceleration =
`\mu g`

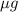
Equation of motion

`v=u+at\\\Rightarrow t=(v-u)/(\mu g)\\\Rightarrow t=(0-6)/(-0.4* 9.81)\\\Rightarrow t=1.52905\ s`

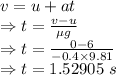
It will take 1.52905 seconds for the block to slow down

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2\mu g)\\\Rightarrow s=(0^2-6^2)/(2* 0.4* -9.81)\\\Rightarrow s=4.58715\ m`

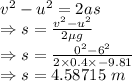
The block will travel 4.58715 m before it stops